
Sadržaj
- Zipfov zakon objasnio je
- Osnovni eksperiment
- Zipfov zakon na tržištima Steam
- Što možemo naučiti o Steamu?
- Zaključci
Nedavno je jedan moj prijatelj predložio da gledam Vsaucesov video o Zipfovom zakonu, Paretovom principu i njihovim tajanstvenim pojavama svuda oko nas. Evo malo zadirkivanja kako bi privukli vašu pažnju - 80% svih ljudi živi u 20% najpopularnijih gradova; 80% zemljišta pripada 20% najbogatijih zemljoposjednika; 80% svih smeća nalazi se na 20% najtrožijih ulica - kao što je to predvidio Zipfov zakon i Paretosovo načelo.
Nedovoljno? Pa, kao što sam jučer otkrio, zečja rupa se tu ne zaustavlja ... Pun skepticizma, odlučio sam pogledati koliko vremena ljudi provode igrajući parne igre ... Pa. 80% vremena ljudi troši na 20% najpopularnijih igara ... Zanimljivo? Pa, čitaj dalje, tu je još nešto u ovoj priči.
Usmjeravanje na više od 20 minuta, Vsauces nastojanje je strašan i objašnjava puno od velike slike stvari o Zipf, ali on je vrlo stidljiv nam pokazuje temeljni mehanizam koji je široko vjeruje da doprinose zašto Zipf radi kako se radi. Dakle, prije nego što nastavimo, želim to ukratko objasniti.
Zipfov zakon objasnio je
Postoji nekoliko konceptualnih načina da se objasni intuicija iza načela 20/80. Najbolji primjer je, po mom mišljenju, onaj o kraterima Mjeseca.
Osnovni eksperiment
Zamislite, ako hoćete, da je netaknuti Mjesec - savršeno glatka površina. Sada, recite da postoje neki slučajno veličinski asteroidi koji udaraju Mjesecom hoćeš-nula. Kada prvi asteroid stigne, ostavlja krater. Sada još jedan pogodi, ostavljajući krater negdje drugdje. Svaki krater je dio ukupne površine, stoga postoji mogućnost da će sljedeći slučajni asteroid pogoditi blizu postojećeg kratera i pridružiti mu se, formirajući skupinu. Vjerojatnost da će novi asteroid pogoditi određeni krater proporcionalan je postojećim veličinama kratera i asteroida. To znači da se sljedeći slučajni asteroid češće pridružuje najvećoj postojećoj grupi, što je čini još većom. Neka vrsta kumulativnog procesa, koji tada stvara bogatiji, bogatiji siromašni mehanizam.
Imajte to na umu jer se vjeruje da je to opće objašnjenje "zašto" zakon Zipfs radi s takvom tajanstvenom univerzalnošću. Primjer asteroida je vrlo jednostavan, no pitanje je što će se dogoditi tijekom mnogih ponavljanja
Malo zbunjujuće?
Pa, napravio sam gif da pokrenem ovu početnu točku kući. NB! o grafikonu ćemo raspravljati kasnije, samo pokušajte zamisliti eksperiment.

Ako promatramo stvarni Mjesec, ispada da, kako se količina asteroida povećava do velikih količina, promjeri kratera rastu tako da se 20% najvećih kratera približava 80% ukupne površine.
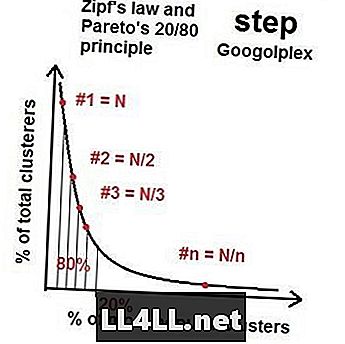
Dakle, kako idemo na više asteroida, distribucija najpopularnijih i najmanje popularnih skupina pristupa nekoj vrsti "idealne distribucije" s ovom svojinom 20/80 - distribucijom Pareta. Ako napravite matematiku, ispada da (općenito), ako najveća grupa ima veličinu N, druga najveća grupa je oko veličine N / 2, treća N / 3 i tako dalje i tako dalje. To se zove Zipfov zakon. Čudna stvar je Zipfov zakon i distribucija Pareta radi za zbunjujuću količinu elemenata (asteroida) i skupina (grozdovi kratera). Naravno, postoje nakošenja i slučajni poremećaji, ali opći trend je neporeciv.
Nadam se da možete vidjeti kako se asteroidi češće udaraju u velike kratere na Mjesecu i povezuju se s gradovima koji su privlačniji, ako već ima više ljudi koji žive u njima. Međutim, čovjek mora shvatiti da su gradovi daleko od samo "skupina" koje se ponašaju prema Zipfu.
Evo nekoliko primjera iz istraživanja Mark Newmans o Pareto distribucijama. NB! Grafovi su u logaritamskoj ljestvici koja izjednačava hiperbolički oblik krivulja, predstavljajući gotovo linearni odnos.
Početno y = aX ^ (- b)
Zapisi obiju strana => log y = log a - b log X
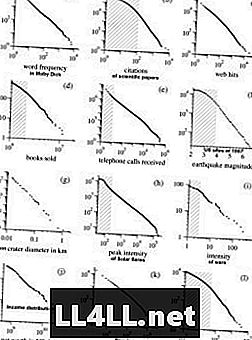
Zanimljivo je da isti trend pokazuju i vjerski kultovi ... Zajednička imovina većine ovih fenomena je jednostavno ta tendencija "velikih skupina-dobivanje-veće". Tako je Zipfov zakon uporan u mehanizmima, gdje su preferencije elemenata pozitivno povezane s veličinom grupa (što znači da što je skupina veća, veća je vjerojatnost da će rasti). Zato volim razmišljati o grupama kao o klasterima i elementima kao o klasterima.
Zipfov zakon na tržištima Steam
Sumnjivo na to posljednje? Ovdje je količina vremena ljudi troše na najpopularnije igre na Steam .. Podaci iz SteamSpy.
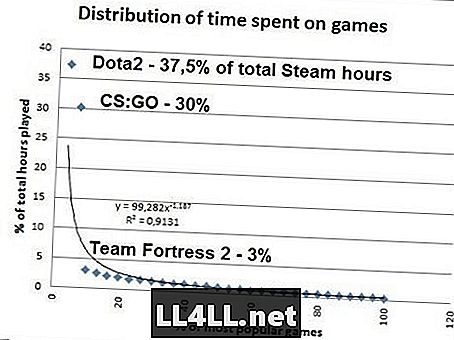
Ako matematiku, ispada da 20% od najpopularnijih Steam igara račun za 80% od ukupnog iznosa igranja, tako da Pareto 20/80 misterija radi kao šarm ovdje ... Jedan mora primijetiti, međutim da za Zipf biti istinit, CS: GO treba iznositi 37,5% / 2 = 18,8% ukupnog vremena umjesto golemih 30%. No, osim ovog outliera (STOP PLAYING) CS: GO), Zipf-slična distribucija je očito tamo.
Evo količine prodanih primjeraka za najpopularnije igre.
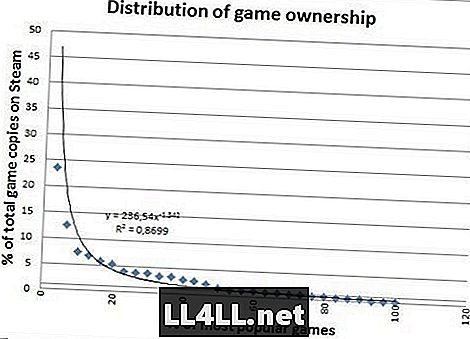
Izgleda ljepše eh? Prodane kopije nemaju velike outliere pa se dobro uklapa, što je značajna razlika. Ipak, postoji nešto zanimljivije što možemo zaključiti iz razlika u zadnja dva grafikona.
Primjećujete li kako je "rep" koji ide desno vrsta masnoće u drugom grafikonu? Pa, jednostavnim riječima, to nam govori da su "relativno nepopularne" igre zapravo mnogo popularnije nego na prijašnjem planu.
Zapravo, ispada da 20% najpopularnijih igara čini samo 60% prodaje, nasuprot 80% igranja. Zanimljiv? Možeš se kladiti da je.
Što možemo naučiti o Steamu?
Pa, činjenica da popularnost igara slijedi Pareto distribuciju nam govori da, doista, postoji neka vrsta pozitivnog učinka Mreže, koji čini igrače odabirom igara koje već igraju više ljudi. Razlika u debljini repa govori nam da su korisnici Steama puno više "slijepi za grupu", kada kupuju igre nego što su kad ih igraju.
Razmislite o tome - što više ljudi kupuje igre bez obzira na "trenutačno popularno mišljenje", to se više raspada Pareto distribucija, jer je manje vjerojatno da će velike igre dalje rasti. Ako nitko nije dao štakorima stražnjicu o tome koliko je ljudi već igralo igru, a dostupnost svih igara bila je ista, očekivali bismo da 20% najpopularnijih igara iznosi oko 50% prodaje i vremena za igru (npr. Ako pretpostavimo da su pojedinačne preferencije normalno distribuiran).
Zaključci
Dakle, postoje dva čimbenika koji doprinose Pareto distribuciji na tržištima Steam - koliko su inovativni razvojni inženjeri (koliko se novih Mjesečevih kratera formira) i koliko igrači (asteroidi) procjenjuju trenutnu veličinu grupe, pri odabiru grupe za pridruživanje , Kako se ispostavilo, igrači su vrlo slijepi za grupu kada kupuju igre, ali upravo suprotno kada ih igraju. Cool huh?
Ako želite saznati više o distribuciji Zakona Law and Power Law, ovdje je lijepo predavanje. Nadalje, pobrinite se da pogledate Newmanov papir!
Ako želite pročitati više o ovoj vrsti stvari, uskoro ću pokušati pridružiti ovo promatranje modelu koji pokazuje da popularnije igre s više igrača imaju veće cijene (koje povezuju s igračima koji žele pridružiti se grupama veće veličine). Pogledajte članak ovdje. U članku Piece De Resistance pokušat će se pridružiti tim teorijama zajedno s objašnjenjem kako su multiplayer igre, društvene mreže i gradovi zapravo anti-rivalska roba s mrežnim efektima, (što više ljudi troši dobro, to više koristi svaki pojedinac) što ima više im je dao ovu zipfijansku maglu misterija ...
Do tada - uživajte!
p.s. Pop u komentar s zabavna ideja za 20/80 odnos mislite da bi moglo biti istinito.
Moje su:
80% nostalgije ljudi uzrokovano je 20% najsretnijih uspomena (dokazano za stopu na kojoj ljudi zaboravljaju)
80% mase je koncentrirano u 20% najvećih svemirskih objekata (zapravo dokazano za distribuciju gravitacijske sile)
I naravno
80% nereda u vašem WC-u dolazi od 20% onoga što jedete (nema akademskih istraživanja o kojima možete govoriti)